Mass in Newtonian theory

So far we have been rather vague about what we mean by the mass  of a body. Even in Newtonian theory we can ascribe three masses to any body which describe quite different properties:

• Inertial mass  : This is a measure of its resistance to change in motion or inertia .
• Passive gravitational mass  : This is a measure of its reaction to a gravitational field.
• Active gravitational mass  : This is a measure of its source strength for producing a gravitational field.

Let us discuss each of these in turn. Inertial mass  is the quantity occurring in Newton's second law [ ]. It is a measure of a body's inertia. Note that as far as Newtonian theory, this mass has nothing to do with gravitation. The other two masses however do.

Passive gravitational mass  measures a body's response to being placed in a gravitational field. Let the gravitational potential at some point be , then if is placed at this point, it will experience a force on it given by

On the other hand active gravitational mass  measures the strength of the gravitational field produced by the body itself. If is placed at the origin, then the gravitational potential at any point a distance r from the origin is given by

We will now see how these three masses are related in the Newtonian framework.

Galileo  discovered in his famous Pisa experiments  [ see Figure 5.3 ] that when two bodies are dropped from the same height, they reach the ground together irrespective of their internal composition.

 
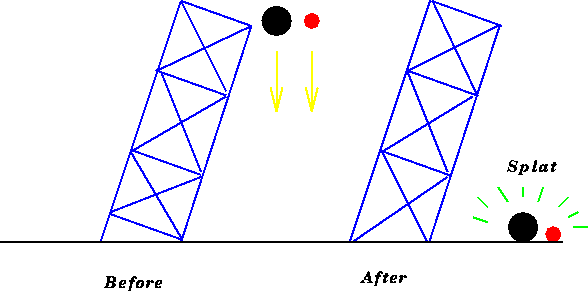
Figure 5.3: The Galileo Piza experiment.

Let's assume that two particles of inertial mass and and passive gravitational mass and are dropped from the same height in a gravitational field. We have:

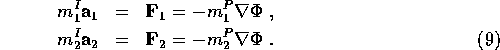
The observational result is from which we get on dividing

Repeating this experiment with other bodies, we see that this ratio is equal to a universal constant say. By a suitable choice of units we can take , from which we obtain the result:

• inertial mass = passive gravitational mass.

This equality is one of the best test results in physics and has been verified to 1 part in .

In order to relate passive gravitational mass to active gravitational mass, we make use of the observation that nothing can be shielded from a gravitational field. Consider two isolated bodies situated at points Q and R moving under their mutual gravitational attraction. The gravitational potential due to each body is

The force which each body experiences is

If we taken the origin to be Q then the gradient operators are

so that

But by Newton's third law , and so we conclude that

and using the same argument as before, we see that

• Passive gravitational mass = active gravitational mass.

That is why in Newtonian theory  we can simply refer to the mass m of a body where

This may see obvious to you, but it has very deep significance and Einstein used it as the central pillar for his equivalence principle .